By Yinggan XU Dibbla
This is generated by a previous courses (not included in Lee’s 2022 series), video can be found: RNN
The RNN aims to deal with sequential inputs. We can first focus on the problem of slot filling:
Time:______ Destination:_____
Here, the Time and Destination are the slots. We could like to automatically fill in the slots with given sentence: I would like to fly to Taipei on Nov 2nd. We have to know “Taipei” is the destination and “Nov 2nd” is the time.
Of course we can use a plain NN to accomplish the task.
- Convert word to vector (1-of-N encoding, word-hashing…)
- Input the word
- Output a distribution indicating which slot the word belongs to
But it’s not enough.
Time:______ Destination:_____ Place of Depart:_____
Given: I’d like to leave New York to Taipei on Nov 2nd. We have to use/memorize the context. Here we use RNN, an NN with “memory”.
graph TB
id1[input1]
id2[input2]
id3[Neuron1 with bias]
id4[Neuron2 with bias]
id5[output Neuron1]
id6[output Neuron2]
id1-->id3
id1-->id4
id2-->id3
id2-->id4
id3-->id5
id3-->id6
id4-->id6
id4-->id5
id7[a1]
id8[a2]
id7-->id3-->id7
id8-->id4-->id8
id7-->id4
id8-->id5
a1, a2 are initialized with certain value, say 0 and all weights are 1. For input [1,1], the Neuron 1&2 with bias both output $(1+1)+(1+1)+0+0=2$, so a1 is 2 and a2 is 2. For second input [1,1], Neuron 1 outputs $1+1+a_1+a_2=6$, Neuron 2 outputs $1+1+a_1+a_2=6$.
So, $$N1 = w_1^Tx+b_1+w_aa = w_1^Tx+b_1+w_{a1}a_1+w_{a_2}a_2$$ $$N2 = w_2^Tx+b_2+w_aa$$
And the whole process works like this:
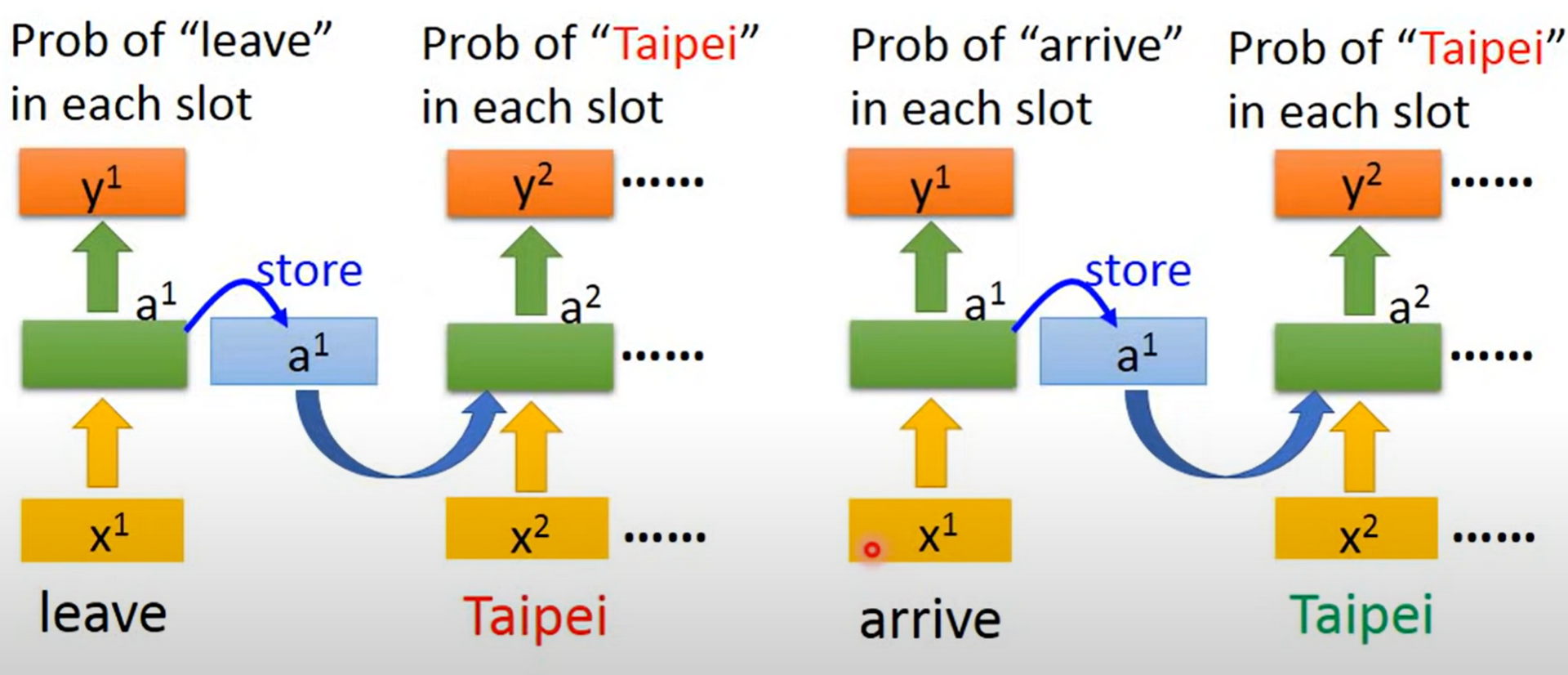
This is called Elman Network, and if the memory stores the final output of the network, it is the Jordan Network.
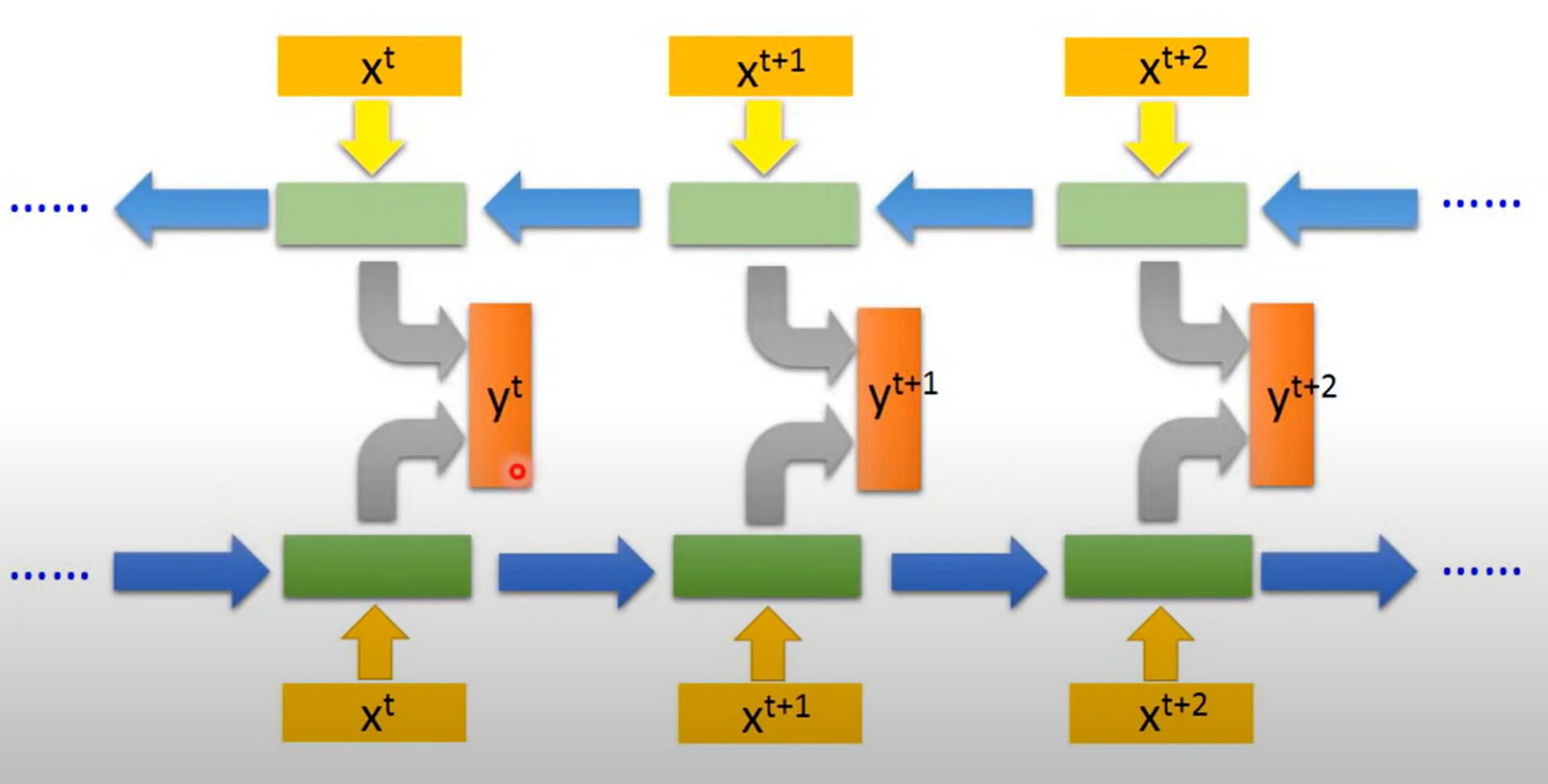
The Network can also be bi-directional: