This is an additional but useful note.
First recap the derivatives for scalars, for example: $\frac{dy}{dx} = nx^{n-1}$ for $y = x^n$. And we all know the rules for different kinds of functions/composed functions.
Note that the derivative does not always exist.
When we generalize derivatives to gradients, we are generalizing scalars vectors. In this case, the shape matters.
| scalar | vector | |
|---|---|---|
| scalar | $\frac{\partial y}{\partial x}$ | $\frac{\partial y}{\partial \textbf{x}}$ |
| scalar | $\frac{\partial \textbf{y}}{\partial x}$ | $\frac{\partial \textbf{y}}{\partial \textbf{x}}$ |
Case 1: y is scalar, x is vector
$$x = [x_1,x_2,x_3,\cdots,x_n]^T$$ $$\frac{\partial y}{\partial \textbf{x}}=[\frac{\partial y}{\partial x_1},\frac{\partial y}{\partial x_2},\cdots,\frac{\partial y}{\partial x_n}]$$
Noted that, x is a column vector and the result is a row vector. Example: $$\frac{\partial}{\partial\textbf{x}}x_1^2+2x_2^2=[2x_1,4x_2]$$ This is like finding a slope in a scalar field, a direction for largest value difference.
For composed function, the rule is basically the same as scalar situation. But if $y=<\textbf{u},\textbf{v}>$, we have $g = \textbf{u}^T\frac{\partial \textbf{v}}{\partial\textbf{x}}+\textbf{v}^T\frac{\partial \textbf{u}}{\partial\textbf{x}}$.
Case 2: y is a vector, x is a scalar
$$\textbf{y}=[y_1,y_2,y_3,\cdots,y_n]^T$$ $$\frac{\partial\textbf{y}}{\partial x}=[\frac{\partial y_1}{\partial x},\frac{\partial y_2}{\partial x},\frac{\partial y_3}{\partial x},\cdots,\frac{\partial y_n}{\partial x},]^T$$
It remains a column.
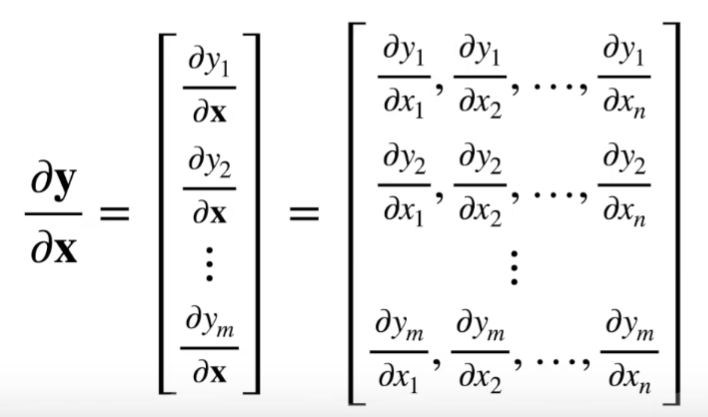
Case 3: Both vector
Suppose $\textbf{x}$ with length $n$, $\textbf{y}$ with length $m$. $$\frac{\partial \textbf{y}}{\partial \textbf{x}}=[\frac{\partial y_1}{\partial\textbf{x}},\frac{\partial y_2}{\partial\textbf{x}},\frac{\partial y_3}{\partial\textbf{x}},\cdots,\frac{\partial y_m}{\partial\textbf{x}}]^T$$
And here we go: